↓タップで拡大↓

(1)は、\(sinA\)を求めてから三角形の面積を求める問題で、以前扱ったものと同様だ。
(2)は内接円の半径を求める問題。三角形と内接円の関係を考えてみる。次の図を見てほしい。
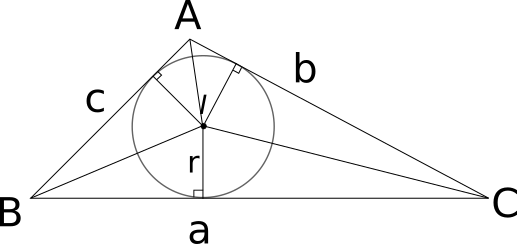
三角形ABCがあり、各辺の長さをそれぞれa,b,cとする。内接円の中心をIとし、半径をrとする。AB,AC,BCそれぞれとIを結ぶ線を引くと、それぞれ角度は90°になる。
ここで三角形ABCの面積を求めたい。三角形BIC,CIA,AIBと3つに分けて考える。それぞれ底辺×高さ×\(\frac{1}{2}\)として計算すると
三角形BICの面積=\(\frac{1}{2}ar\)
三角形CIAの面積=\(\frac{1}{2}br\)
三角形AICの面積=\(\frac{1}{2}cr\)
となる。よって三角形ABCの面積Sは
\(S=\frac{1}{2}ar+\frac{1}{2}br+\frac{1}{2}cr\)
右辺を\(\frac{1}{2}r\)でくくると
\(S=\frac{1}{2}r(a+b+c)\)
少し形を変えて
\(S=\frac{1}{2}(a+b+c)r\)
とし、公式が完成する。