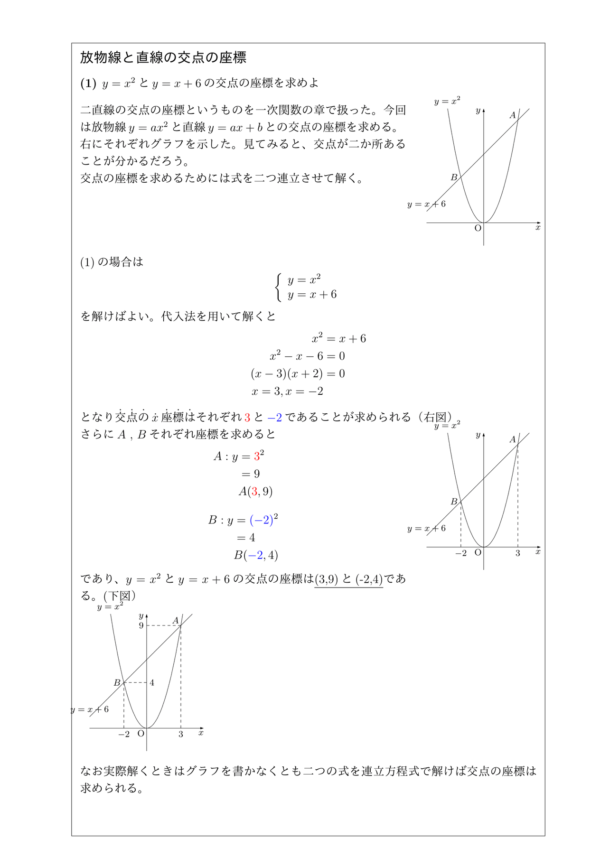
「二直線の交点の座標を求めるには、二つの直線の式の連立方程式を解けばいい」ということは、一次関数を習った段階で学ぶ。本問は、それが「放物線と直線の交点」となっているだけであり、考え方は実は全く同じなのだ。つまり「放物線の式を直線の式の連立方程式を解けば」交点の座標が求められる。
ただし放物線の式というものは二乗が入っているため、連立して代入法で解く際に、二次方程式を解くことになる。二次方程式は解が2つあるため、それが二点のx座標をそれぞれ表している点に注目する。グラフを見れば分かるが、放物線と直線だと、交点が2か所あるため、連立方程式の解も二つあるのである。
ちなみに、問題にグラフが書いていない場合でも、グラフの概形を書くことによって求めやすくなる。