問1

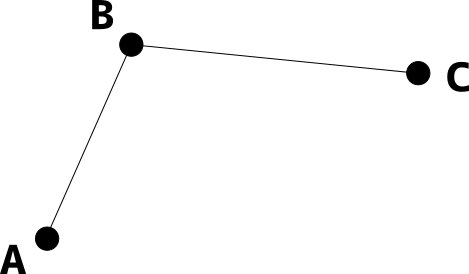
3点ABCを通る円を作図せよ、という問題がある。書き方を考えてみよう。
まず、円を描くためには何が必要か?当然コンパスだ。コンパスを使うには、「どこに針を置くか」が分からないと円が書けない。上の問題でも、闇雲に針を置いて試してみても、恐らくうまくいかないだろう。
なので、コンパスの針を置く場所、すなわち円の中心がどこにあるのかを見つけなければならない。
ABCを通る円がある、ということは、その円の中心はAからもBからもCからも等しい距離にある、と考えることが出来る。
点A,点B,点Cから等しい距離にある点を探す。これは、垂直二等分線の出番である。
AB,BCに線を引き
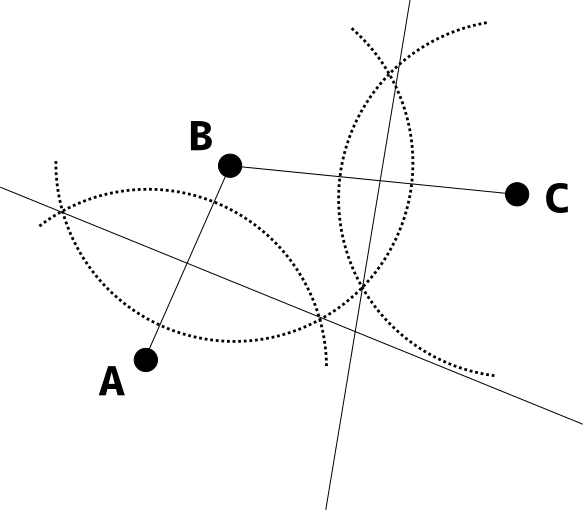
それぞれ垂直二等分線を描く。そして二本の垂直二等分線が交わっている地点が、円の中心となる。なので、その部分に針を置けばいい。

完成!
問2
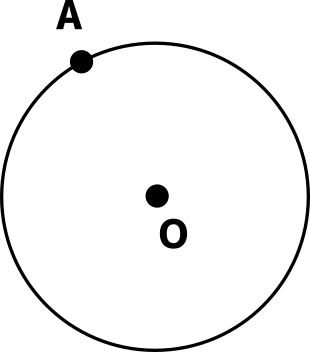
点Aを通り、円Oに接する線を作図せよ、という問題がある。円に接する線を接線と言い、円と接線が交わる場所を接点という。今回の問題で言えば、点Aにあたる部分が接点となる。
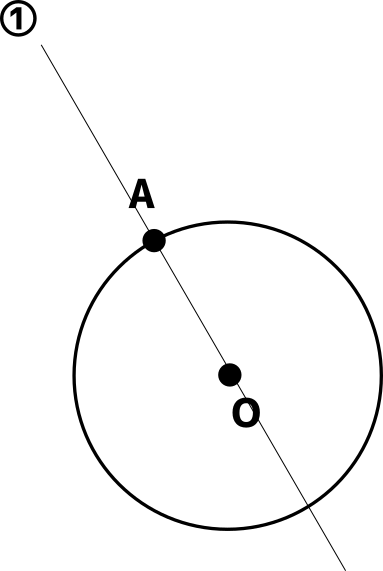
①:円の中心と接点を通る直線を描く
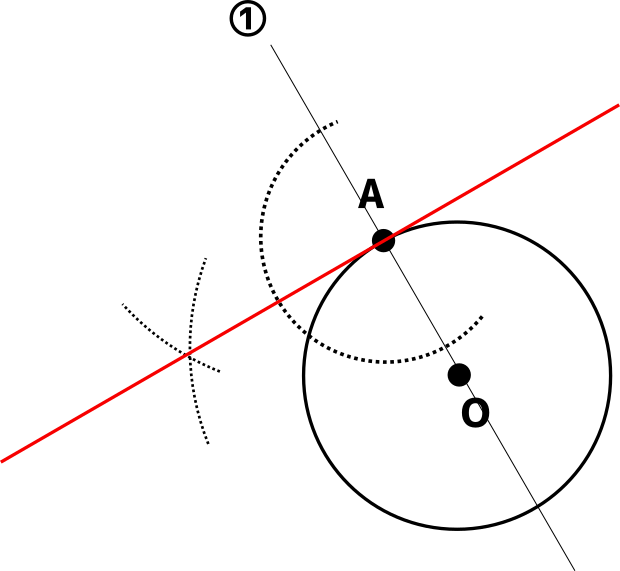
点Aを通り、①で描いた線に垂直な線を描く。この赤い線が、点Aを通る円Oの接線である。
完成図を見てもらえば分かるが、円の接線と、接点と中心を結んだ線(直線AO)は垂直に交わる。このことは、角度を求める問題などでもよく使われるので覚えておこう。